Doğal sayılar

Doğal sayılar, $mathbb{N} = { 0, 1, 2, 3, 4, 5, 6, 7, ... }$ şeklinde sıralanan tam sayılardır. Negatif değer almazlar. Bazı kaynaklarda "0" doğal sayı olarak alınmaz. Matematikte hala sıfırın bir doğal sayı alınıp alınmayacağı tartışma konusudur, ancak eğer cebirsel inşâlar yapılmak isteniyorsa "0" sayısının doğal sayı olarak alınması avantaj sağlayabilir. Matematiğin diğer dallarında da problem hangi durumda daha kolay ifade edilebilecekse doğal sayılar kümesi de o şekilde alınır.

Sayı değeri

Bir doğal sayının rakamlarının belirttiği değere rakamların sayı değeri denir. Doğal sayının rakamlarının toplamına rakamların sayı değerleri toplamı denir.

Basamak değeri

9 basamaklı bir doğal sayının basamaklarının değerleri

Birler basamağının basamak değeri : 1
Onlar basamağının basamak değeri : 10
Yüzler basamağının basamak değeri : 100
Binler basamağının basamak değeri : 1.000
On binler basamağının basamak değeri : 10.000
Yüz binler basamağının basamak değeri : 100.000
Milyonlar basamağının basamak değeri : 1.000.000
On milyonlar basamağının basamak değeri : 10.000.000
Yüz milyonlar basamağının basamak değeri : 100.000.000

Onlu sayma düzeninde bir basamağın değeri sağındaki basamağın 10 katıdır.

Bir rakamın basamak değeri o rakam ile rakamın yazıldığı basamağın çarpımıyla bulunur..

12345 sayısındaki 2 nin basamak değeri 2 (sayı değeri) ve 1000 (basamak değeri) çarpılarak 2 X 1000 2000 şeklinde bulunur.

Peano Belitleri tanımı

Peano belitleri tarihsel olarak doğal sayıların en genel (ve sezgisel) tanımıdır. Modern tanımlar bu tanımı sağlar.

Sıfır bir doğal sayıdır.
Her doğal sayının, yine bir doğal sayı olan bir ardılı vardır.
Ardılı sıfır olan hiç bir doğal sayı yoktur.
Ardılları eşit olan doğal sayılar da birbirine eşittir.
Doğal sayılardan oluşan bir küme, sıfırı ve her doğal sayının ardılını içeriyorsa o küme doğal sayılar kümesine eşittir.

Sıfırı doğal sayı olarak kabul etmeyen grup, buradaki belitlerin "Bir, bir doğal sayıdır." olarak kabul eder.

ZFC tanımı

Zermelo-Freankel küme kuramı) doğal sayılar, von Neumann sıral sayılarıyla inşa edilebilir. Buna göre her sayı temelde bir kümedir. Eğer sıfır boşküme olarak tanımlanırsa ve her n sayının ardılı, $n +$ , n $cup$ {n} olarak verilirse, doğal sayılar inşa edilmiş olur.

$0=emptyset$

$n^+ = n cup { n }$

Bu tanım doğal sayıların yinelgen bir yapıda olduğunu da belirtmiş olur. Bu yinelgen tanımla sayılar,

0={}

1={0}

2={0,1}

3={0,1,2}

...

n+1={0,1,...,n}

Bu tanımda iki doğal sayının eşitliği sayıların öğe sayısına dayanır.

Russell'ın farklı bir tanımı daha genel görünebilir:0 DOĞAL SAYIDIR

$0={emptyset}$ (sıfır, hiç öğesi olmayan tüm kümelerin kümesi)

$n^+ = { x cup { y } , | , x in n , text{ve} , y notin x }$ (n nin ardılı, öğe sayısı n olan tüm kümelerin kümesi)

Ne var ki bu tanım belitsel küme kuramlarında geçerli değildir, çünkü bir sayı, küme olamayacak kadar büyük topluluklar olmak zorunda kalıyor. Ancak tipler kuramı gibi kuramlarda geçerlidir.

Büyüklük ve küçüklük ilişkileri

Doğal sayıların sıralanmasına en büyük basamaktan başlanır. Aynı basamakta büyük rakam bulunan sayı diğerinden büyüktür.

İki sayının yüz milyonlar basamaklarında eşit rakamlar bulunuyor. Bu nedenle karşılaştırma bir sonraki basamak olan on milyonlar basamaklarında yapılır. Bu basamaklarda 9 > 8 olduğundan 894.125.067 > 887.954.700 yazılır. “ 894.125.067 büyüktür 887.954.700 şeklinde okunur.”

N = {0,1,2,3,4,5,6,7,8,9} Doğal Sayılar Kümesinde; iki doğal sayının toplamı yine bir doğal sayı olur.

Doğal sayılarda işlemler

Doğal sayılar toplama ve çarpma işlemine göre kapalıdırlar. İki doğal sayının çarpımı veya toplamı yine bir doğal sayıdır. Örneğin : 3.5=15 , 7.9=63 İki doğal sayının farkı veya bölümü bir doğal sayı olmayabilir bu nedenle doğal sayılar çıkarma ve bölme işlemine göre kapalı değildir. Örn: 9-12 = -3 , 2/4 = 1/2 gibi.

Toplama işlemi

Toplama işlemi ileri doğru sayma işlemidir. Toplama işlemine katılan sayılara terim, işlemin sonucuna toplam denir. Toplama işlemi sayıların aynı basamakları arasında yapılır. Bu nedenle toplama işleminde sayılar aynı basamaklar alt alta gelecek şekilde yazılır.

Doğal sayılarda toplama aşağıdaki cebirsel kurallara uyar:

Toplamsal birim öğe:

a + 0 = a

Toplamanın değişme özelliği:

a + b = b + a

Toplamanın birleşme özelliği:

(a + b) + c = a + (b + c)

Toplamanın çarpma üzerine dağılma özelliği (sağdan dağılma):

(a + b)c = ac + bc

Bir a sayısını bir b sayısıyla toplamak, a sayısının b kere ardılını almak olarak tanımlanır. Daha matematiksel bir tanım verilmek istenirse $A r d (n)$ gösterimi n sayısının ardılını ifâde etmek üzere, toplama aşağıdaki belitlerle tanımlanır:

$a + 0 = a$
$a + A r d (b) = A r d (a + b)$

Bu belitlerden yola çıkarak ardıllık işlemini toplama cinsinden göstermek mümkündür: 2. belitte b=0 seçilirse

a + A r d (0) = a r d (a + 0)

sıfırın adrılı birdir, o halde,

A r d (a) = a + 1

olduğu kolaylıkla görülür.

Çarpma işlemi

Çarpma işlemi ard arda toplama işlemidir. Çarpma işlemine katılan sayılara çarpan, işlemin sonucuna çarpım denir.

Doğal sayılarda çarpma aşağıdaki cebirsel kurallara uyar:

Çarpımsal birim öğe:

a1 = a

Çarpmanın değişme özelliği:

ab = ba

Çarpmanın birleşme özelliği:

(ab)c = a(bc)

Çarpmanın toplama üzerine dağılma özelliği (soldan dağılma):

c(a + b) = ca + cb

Bir a sayısını bir b sayısıyla çarpmak, a sayısının b kere toplamını almak olarak tanımlanır. Daha matematiksel bir tanım verilmek istenirse $A r d (n)$ gösterimi n sayısının ardılını ifâde etmek üzere, çarpma aşağıdaki belitlerle tanımlanır:

$a 1 = a$
$a , Ard(b) = ab + a$

E.B.O.B. – E.K.O.K.

A. ASAL SAYILAR 1 ve kendisinden başka hiçbir sayma sayısı ile bölünemeyen 1 den büyük doğal sayılara asal sayılar denir.

2, 3, 5, 7, 11, 13, 17, 19 sayıları 1 ile 20 arasındaki asal sayılardır.

2 den başka çift asal sayı yoktur.
0 ve 1 doğal sayıları asal sayı değildir.
Bir sayının asal sayı olup olmadığını anlamak için küçükten büyüğe kendisinden önceki asal sayılara bölünüp bölünmediğini kontrol etmemiz gerekir.

B. ARALARINDA ASAL SAYILAR 1 den başka pozitif ortak böleni olmayan doğal sayılara aralarında asal sayılar denir.

C. BİR DOĞAL SAYIYI ASAL ÇARPANLARINA AYIRMA 12 sayısının tüm çarpanlarının kümesini yazalım:

1, 2, 3, 4, 6, 12

Bu çarpanların bazıları asal, bazıları da değildir. Buradan şu sonucu çıkarabiliriz. Doğal sayının çarpanlarından asal olanlarına, bu doğal sayının asal çarpanları denir. Bir doğal sayı asal çarpanlarının çarpımı şeklinde yazılabilir.

D. BİR DOĞAL SAYININ BÖLENLERİ (ÇARPANLARI) Bir doğal sayıyı kalansız olarak bölen sayma sayılarına, o sayının bölenleri denir.

Herhangi bir doğal sayının bölenleri aynı zamanda o sayının çarpanlarıdır. Her doğal sayı, kendi çarpanlarına kalansız bölünür.

E. BİR TAM SAYININ TAM BÖLENLERİ a, b, c birbirinden farklı asal sayılar ve m, n, k pozitif tam sayılar olmak üzere,

A = a^m . bⁿ . c^k olsun.

A yı tam bölen asal sayılar a, b, c dir.
A sayısının pozitif tam bölenlerinin sayısı:

(m + 1) . (n + 1) . (k + 1) dir.

A sayısının pozitif tam bölenlerinin ters işaretlileri de negatif tam bölenleridir.

F. EN BÜYÜK ORTAK BÖLEN (E.B.O.B.)

Bir sayı, iki farklı doğal sayının böleni ise, buna doğal sayıların ortak böleni denir.

İki ya da daha fazla sayma sayısının ortak bölenleri arasında en büyük olanına, bu sayıların en büyük ortak böleni denir ve e.b.o.b. biçiminde gösterilir.

E.b.o.b. bulunurken verilen sayıları aynı anda bölen asal sayıların çarpımı bu sayıların e.b.o.b. unu verir.
İki veya daha fazla doğal sayının e.b.o.b. u bu sayıların ortak asal çarpanlarının her birine, ayrı ayrı bölünür.

G. EN KÜÇÜK ORTAK KAT (E.K.O.K.) Bir sayı iki farklı doğal sayının katı ise, buna doğal sayıların ortak katı denir.

İki ya da daha fazla sayma sayısının ortak katları kümesinin en küçük elemanına, bu sayıların en küçük ortak katı denir ve (e.k.o.k.) biçiminde gösterilir.

İki sayma sayısının çarpımı, bu sayıların e.b.o.b. u ile e.k.o.k. unun çarpımına eşittir. Fakat ikiden fazla pozitif tam sayının çarpımı, bu sayıların e.b.o.b. u ile e.k.o.k. unun çarpımına eşit olmayabilir.

A x B = (A; B)_e.b.o.b. x (A; B)_e.k.o.k.şeklindedir.

A ile B aralarında asal ise,

(A; B)_e.b.o.b. = 1

(A; B)_e.k.o.k. = A x B dir.

A ve B sayma sayıları ve A < B olmak üzere;

(A; B)_e.b.o.b. £ A < B £ (A; B)_e.k.o.k.şeklindedir.

Rasyonel sayılar

Rasyonel Sayılar ( , rasyonel veya oranlı sayılar (veya kesirler) iki tamsayının birbirine oranı ile ifade edilebilen sayılardır. Oranlı sayılar b sıfır olmamak üzere a/b şeklinde (a ve b tamsayı) yazılabilir. 2/3 ve 4/6 veya 6/9 eşdeğer oranlı sayılardır. Dolayısıyla her oranlı sayı sonsuz şekilde ifade edilebilir. Oranlı sayıların en basit formu a ve b tamsayılarının ortak böleninin olmadığı a/b ifadesidir.

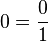Her tam sayı oranlı sayıdır. Çünkü $-3=frac{-3}{1}$ veya $0=frac{0}{1}$ veya $43=frac{43}{1}$ şeklinde yani oranlı sayı tanımına uygun biçimde yazılabilirler. Oranlı sayılar kümesi $mathbb{Q}$ , tam sayılar kümesi $mathbb{Z}$ 'yi kapsar. Yani $mathbb{Z} subset mathbb{Q}$ .

Tanım Oranlı sayılar kümesi, tam sayıların bir genişlemesidir ve Q ile veya $mathbb{Q}$ ile gösterilir. $mathbb{Q}$ kümesi genelde şöyle tanımlanır:

$mathbb{Q} = left{frac{m}{n} : m in mathbb{Z}, n in mathbb{Z}, n ne 0 right}$

Daha ince bir tanımı ise tam sayılar üzerinden tanımlanacak bir denklik bağıntısıyla yapılabilir. Böylece her denklik sınıfı bir oranlı sayı olarak anılır. $mathbb{Z} times mathbb{Z}$ kümesinden seçilmiş keyfî (a,b) ve (c,d) öğeleri için "~" bağıntısı

$(a,b) sim (c,d) Leftrightarrow ad=bc, quad b,d not= 0$

olarak tanımlansın. Bunun bir denklik bağıntısı olduğu kolaylıkla kanıtlanabilir. Bu durumda, denklik sınıfları

$overline{(a,b)} = {(a,b) | (a,b) sim (c,d) }$

olurlar. Oranlı sayı ise basitçe

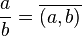
$frac{a}{b} = overline{(a,b)}$

şeklinde tanımlanır.

Tanımda paydanın sıfır olmama şartı $frac{a}{0}$ ifadesinin tanımlanmamış olmasındandır. Bir sayının sıfıra bölümü tanımsızdır.

Oranlı sayıların cebirsel özellikleri

Toplama belitleri

Toplamsal birim öğe:

$q=frac{a}{b}$ bir oranlı sayı ise a=0 olduğunda q toplamanın birim öğesidir ve 0 ile gösterilir.

p + 0 = p

Toplamsal tersinir öğe:

 ve  iki oranlı sayı olsun. Eğer ad=-bc ise bu iki sayı birbirinin toplamsal tersidir.

p + (-p) = 0

Toplamada değişme özelliği:

p+q = q+p

Toplamada birleşme özelliği:

Toplamanın çarpma üzerine dağılma özelliği (sağdan dağılma):

(p + q)r = pr + qr

Çarpma belitleri

Çarpımsal birim öğe:

$q=frac{a}{b}$ bir oranlı sayı ise a=b olduğunda q çarpmanın birim öğesidir ve 1 ile gösterilir.

p1 = p

Çarpımsal tersinir öğe:

$frac{a}{b}$ ve $frac{c}{d}$ iki oranlı sayı olsun. Eğer ac=bd ise bu iki sayı birbirinin çarpımsal tersidir.

p(p^-1) = 1

Çarpmada değişme özelliği:

2+61+

Çarpmada birleşme özelliği:

(pq)r = p(qr)

Çarpmanın toplama üzerine dağılma özelliği (soldan dağılma):

r(p + q) = rp + rq

Oranlı sayıların eşitliği

İki oranlı sayının eşitliği, o sayıların pay ve paydalarının oranlı olmasıyla anlaşılır. $a,b,c,d in mathbb{Z}$ olmak üzere $frac{a}{b}$ ve $frac{c}{d}$ iki oranlı sayı ise bu iki sayı ancak ad=bc olduğunda eşittir.

Bu koşul, yukarıdaki tanımdan çıkarsanabilir. İki oranlı sayı aynı denklik sınıfındaysa birbirine eşittir, Denklik bağıntısı da zaten ad=bc koşulunu içermekteydi.

Rasyonel Sayilar ve Özellikleri

Rasyonel ve irrasyonel sayılar:

Birbirine denk olan kesirlerin meydana getirdiği her kümeye rasyonel sayı denir. Rasyonel sayıların meydana getirdiği kümelere rasyonel sayılar kümesi denir. Rasyonel sayılar kümesi “Q” ile gösterilir.

NOT: Her tam sayı rasyonel sayı olarak yazılabilir.

ÖR:

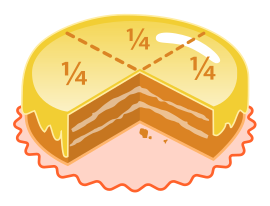
Dörde bölünüp, dörtte biri kesilip alınmış ve geri kalan dörtte üçü gösterilen bir yuvarlak pasta

Yandaki şekilde,bir bütün yuvarlak pasta 4 eş parçaya bölünmüş ve bu 4 eş parçalardan her birisi

olarak görülmektedir. Ancak bir parça alınmış olduğundan kalan eksikdir. Geriye kalan, dört eşit parçaya bölünmüş bütünün üç tane parçası (yani 3de 4 oranı) veya (kesiri)dir. Bu

ifadesi şeklinde gösterilir. Burada ifadede kesir çizgisinin üstündeki değere (yani 3e) pay, kesir çizgisinin altındaki değere (yani 4’e) payda denir. Bu kesir, “üç bölü dört” ya da “dörtte üç” diye okunur.

NOT: Sıfırdan büyük olan rasyonel sayılara pozitif rasyonel sayılar, sıfırdan küçük rasyonel sayılar da negatif rasyonel sayılar denir.

Pozitif rasyonel sayılar kümesi “Q+”ile gösterilir. Negatif rasyonel sayılar kümesi”Q-“ile gösterilir.

Q =  Q- Q+ {0} U  Q+

İrrasyonel sayılar:

Sayı doğrusu üzerinde görüntüsü olmasına karşın,rasyonel olmayan gibi sayılara irrasyonel sayılar denir.İrrasyonel sayıların oluşturduğu kümeye irrasyonel sayılar kümesi denir.

Gerçek (reel) sayılar kümesi:

Rasyonel sayılar kümesi ile irrasyonel sayıların birleşim kümesine gerçek (reel) sayılar kümesi denir.Gerçek sayılar kümesi , gercek sayi ekseninin her noktasını doldurur. Sayı doğrusu üzerinde her noktaya bir gerçek sayı her gerçek sayıya da bir nokta karşılık gelir. Gerçek sayılar kümesi,”R” sembolü ile gösterilir.

Rasyonel Sayıları Karşılaştırma (büyüklük ,küçüklük)

Paydaları eşit olan rasyonel sayılar:

Paydaları eşit olan rasyonel oranlar icin payı büyük olan daha büyük, payı küçük olan daha küçüktür.

Örneğin:

(7/20) > (3/20) Burada paydalar eşit ve 20dir. Pay değerleri karşılaştırılınca soldaki pay 7 sagdaki pay 3 den daha büyük oldugu için, soldaki rasyonel oran daha büyüktür.

Unutmamalıdır ki negatif paylar karşılaştırılırken sadece mutlak değerlerin karşılaştırılması hatalı olup negatif işaretlerinin de ele alınması ve negatif sayılı pay değerlerde mutlak değeri büyük görünen sayının daha küçük olduğu hatırlanmalıdır:

Örneğin:

( -7|20 ) < ( -3/20 )

Payda 20ye eşit olup sağda ki negatif pay değeri -3, sağdaki negatif pay değeri olan -7den daha büyük olduğu için sağdaki oran daha büyüktür.

Arada olma

İki rasyonel sayı arasına bir ya da birkaç rasyonel sayı yerleştirme işlemine denir.

ÖR:    2/3    ile     4/5

I.YOL: 2 4 II:YOL:2 4 III.YOL: 1 2 4

3  .     5                    3  .     5                          2  .    3   .   5
                 2  .

1 2 4 1 10 12 1 22 22 2 3 5 2 15 15 2 15 30

ÖR: 5 ile 7 1 5 7 1 15 14

4            6         2        4        6        2        12       12
                                                  
                                                  1      29       29
                                                  2      12       24

5 29 7 4 24 6

=Rasyonel Sayilarda Toplama İşlemi

Aynı işaretli iki rasyonel sayının toplama işlemi

Aynı işaretli iki rasyonel sayının toplama işlemi yapılırken ,rasyonel sayıların paydaları eşit değilse, paydalar eşitlenir. Payların mutlak değerleri toplamı paya yazılır.Ortak payda,paydaya yazılır.toplananların ortak işareti,toplama ,işaret olarak verilir.

Tam sayılı kesirler toplanırken , bu kesirler bileşik kesre çevrilerek toplama işlemi yapılır.

ÖR: +3 +7 +3 +35 +3 +38

5        1        5        35         3         5

Ters işaretli iki rasyonel sayının toplama işlemi

Ters işaretli iki rasyonel sayının toplama işlemi yapılırken, rasyonel sayıların paydaları eşit değilse eşitlenir.payların mutlak değerleri farkı alınır,paya yazılır.Ortak payda ,paydaya yazılır.toplam olan rasyonel sayının işareti ise,mutlak değeri büyük olan rasyonel sayının işaretidir.

ÖR: 1 2 1 20 24 15

3     5      4      60      60      60
                               
                             
                                 +20+24+(-15)
                                          60
                                
                                  +44+(-15)
                                        60
                                
                                   29
                                   60

Rasyonel Sayilar Kumesinde Toplama Isleminin Özellikler

Kapalılık özelliği:

İki rasyonel sayının toplamı , yine bir rasyonel sayıdır.Yani rasyonel sayılar kümesi toplama işlemine göre kapalıdır.

ÖR: - 2 + 2 -4 +2 -2

3           6           6           6           6

Değişme özelliği:

Rasyonel sayılar kümesinde,toplama işleminin değişme özelliği vardır.

ÖR: -4 +1 -8 +7 -1

7            2          14           14         14

+1          -4          +7          -8           -1
                2            7           14         14           14

-4            +1               +1              - 4
               7               2                 2                 7

Birleşme özelliği:

Rasyonel sayılar kümesinde toplama işleminin birleşme özelliği vardır.

ÖR: 4 3 1 4 4 8

5             5             5            5          5                 5

4             3            1            7           1               8
              5             5            5            5           5               5

4         3        1           4        3        1
                     5         5        5           5        5        5

Etkisiz (birim) eleman özelliği:

”0” tam sayısına, rasyonel sayılar kümesinde toplama işleminin etkisiz (birim )elemanı denir.

ÖR: -7 -7 -7 -7

9                9                                 9                 9

buna göre;

-7                               -7
                                  9                                9

Ters eleman özelliği:

Toplamları “0”tam sayısına eşit olan iki rasyonel sayıya toplama işlemine göre birbirinin tersi denir.

ÖR: +5 -5 20 20

-5             +5
               20            20

Rasyonel Sayilarda Çikarma İslemi

İki rasyonel sayının farkı bulunurken, eksilen rasyonel sayı,çıkan rasyonel sayının toplama işlemine göre tersidir.

ÖR: +3 +1 +3 -1 +18 -5 +13

5           6            5           6            30         30             30

ÖR: +7 +5 +7 +25

10             2             10             10
                                              
                                              +7           -25            -18
                                               10            10             10

Yukarıda verilen örneğe göre iki rasyonel sayının farkı,yine bir rasyonel sayıdır.Buna göre rasyonel sayılar kümesi çıkarma işlemine göre kapalıdır.

Rasyonel Sayilarda Çarpma İslemi

İki rasyonel sayının çarpma işlemi payların çarpımı paya,paydaların çarpımı paydaya yazılarak yapılır.

NOT:Aynı işaretli iki rasyonel sayının çarpımı pozitif , ters işaretli iki rasyonel sayının çarpımı ise negatif bir rasyonel sayıdır.
    Yani:       
                      +  x  + = +
                      -  x  - = +
                      -  x  + = -
                      +  x  - = -
 

ÖR:        -4        +3          (-4)x(+3)             -12
                1          4             1 x 4                    4

NOT:Tam sayılı kesir biçminde verilen rasyonel sayılar çarpılırken önce tam sayılı kesirler bileşik kesre çevrilir.Sonra çarpma işlemi yapılır.

Rasyonel Sayilar Kumesinde Çarpma İsleminin Özellikleri

Kapalılık özelliği:

İki rasyonel sayının çarpımı yine bir rasyonel sayıdır.Yani rasyonel sayılar kümesi çarpma işlemine göre kapalıdır.

ÖR: +3 -2 -6

4              3              12

Değişme özelliği:

Rasyonel sayılar kümesinde carpma işleminin değişme özelliği vardır.

ÖR: -19 -1 +19

20           3              60

-1         -19           -19
                3           20            60

Birleşme özelliği:

Rasyonel sayılar kümesinde çarpma işleminin birleşme özelliği vardır.

ÖR: +3 -2 +1 -6 +1 -6

1          3              5           3             5             15
    
     +3         -2            +1         +3            -2            -6
                1          3               5           1             15           15

Yutan eleman:

Bir rasyonel sayının “0”sayısı ile çarpımı “0”dır. ”0”sayısına ,çarpma işleminin yutan elemanı denir.

ÖR: -7 -7 9 5523

Etkisiz birim eleman:

+1 rasyonel sayısına, çarpma işlemine göre etkisiz (birim) eleman denir.

örnek:0 0 0 0

Ters eleman:

Çarpımları +1 olan iki rasyonel sayıya çarpma işlemine göre tersi denir.

ÖR: +2 +3 2 x 3 +1

3                  2               3 x 2              1

Çarpma işleminin toplama işlemi üzerine dağılma özelliği:

Rasyonel sayılar kümesinde , çarpma işleminin toplama işlemi üzerine dağılma özelliği vardır.

ÖR: +1 +2 +1 +1 +3 +3

2         4          4              2            4           8

+1            +2         +1        +1        +2         +1        +1
                2               4          4           2          4           2           4

+2                 1                   +3
                                                         8                 8                     8

Çarpma işleminin çıkarma işlem üzerine dağılma özelliği:

Rasyonel sayılar kümesinde , çarpma işleminin çıkarma işlemi üzerine dağılma özelliği vardır.

ÖR: 1 2 1 1 1 1

2     4      4         2      4       8
              
              1         2         1         1         2         1        1
              2         4         4         2         4         2        4

2 1 8 8

1
                                               8

Rasyonel Sayılarda Bölme İşlemi

İki rasyonel sayının bölme işlemi yapılırken, bölünen rasyonel sayı , bölen rasyonel sayının çarpma işlemine göre tersi ile çarpılır.Elde edilen çarpım bölümü verir.

NOT:Aynı işaretli iki rasyonel sayının bölümü pozitif; ters işaretli ki rasyonel sayının bölümü ise negatif bir rasyonel sayıdır.

  Yani:           +  . + = + 
                  -  . - = +
                  -  . + = -
                  +  . - = -

ÖR: -3 +2 -3 +4 -3

               4              4             4                  2             2

+1 tam sayısının , bir rasyonel sayıya bölünmesinden elde edilen bölüm,bölen rasyonel sayının çarpma işlemine göre tersine eşittir.

ÖR: -2 1 -7 -7

                            7             1                2               2

(-1)tam sayısının, bir rasyonel sayıya bölünmesinden elde edilen bölüm bölen rasyonel sayının çarpma işlemine göre tersinin ters işaretlisine eşittir.

 ÖR:                 12                   +17         17
                         17                     12         12

Bir rasyonel sayının , +1 tamsayısına bölünmesinden elde edilen bölüm , rasyonel sayının kendisine eşittir.

Bir rasyonel sayının,(-1) tamsayısına bölünmesinden elde edilen bölüm , bölünen rasyonel sayının toplama işlemine göre tersine eşittir.

ÖR: -2 -2 1 -2 1 -2

               7                 7                1               7            1             7

ÖR: -2 -2 -1 -2 -1 2

               7                  7                1              7         1                7

NOT: Sıfır sayısının , sıfırdan farklı olan her rasyonel sayıya bölümü ”0” dır.

Bir rasyonel sayının sıfıra bölümü tanımsızdır.

Rasyonel sayılar kümesinde bölme işleminde , doğal sayılar ve tam sayılar kümesindeki bölme işleminde olduğu gibi; ”bölünen = pay . payda” ilişkisi vardır.

NOT:Rasyonel sayılar kümesi , bölme işlemine göre kapalıdır.

NOT:Rasyonel sayılar kümesinde , bölme işleminin değişme özelliği yoktur.

NOT:Rasyonel sayılar kümesinde , bölme işleminin birleşme özelliği yoktur.